并集和交集是集合常见的集合及其区别的常用概念并集并集是指两个集合的所有元素的总和它表示两个集合中的所有元素常见的集合及其区别,不管这些元素是否在另一个集合中出现过交集交集是指两个集合中共有的元素它表示两个集合中共同存在的元素因此常见的集合及其区别,并集和交集的区别在于并集描述了两个集合中所有元素的总和,而交集描述了两个常见的集合及其区别;集合和聚合确实存在区别以下是两者的主要差异集合 定义在数学上,集合是指若干具有共同属性的事物的总体例如,全部整数构成一个整数的集合,一个工厂的全体工人构成一个该工厂全体工人的集合 语境在日常语境中,集合也常用于描述许多分散的人和物聚在一起的状态,如“全校同学已经在操场集合。
JAVA集合中ListSet与Map的区别如下1 List 特点List是一个有序的集合,允许存储重复的元素,并且每个元素都有一个索引 常用实现 ArrayList基于数组实现,查找效率高,但插入和删除特定位置的元素效率较低 LinkedList基于链表实现,插入和删除效率高,但查找效率相对较低 Vector;4补集 一般地,设S是一个集合,A是S的一个子集,由S中所有不属于A的元素组成的集合,叫做子集A在S中的绝对补集记作#8705UA,包括三层含义1A是U的一个子集,即A#8842U2#8705UA表示一个集合,且#8705UA#8842U3#8705UA是由U中所有不属于A的元素组成的集合;集合主要有Collection和Map接口List特点元素有放入顺序,元素可重复 Map特点元素按键值对存储,无放入顺序 Set特点元素无放入顺序,元素不可重复注意元素虽然无放入顺序,但是元素在set中的位置是有该元素的HashCode决定的,其位置其实是固定的List接口有三个实现类LinkedList,ArrayList,Vector;例如,“树”“书”“中国”在泛指国家整体而非特指某个具体事件或群体时等都是非集合概念 特征非集合概念关注的是事物的个体性或类别性,而不是它们的集合性它强调的是事物本身的属性或类别归属,而不是事物之间的共同属性或整体性注意事项 集合概念和非集合概念的区分并不是。
数学上一些常用的数集及其记法所有正整数组成的集合称为正整数集,记作N*,Z+或N+ 集合简称集是数学中一个基本概念,它是集合论的研究对象,集合论的基本理论直到19世纪才被创立最简单的说法,即是在最原始的集合论朴素集合论中的定义,集合就是“一堆东西”集合里的“东西”,叫;根据对等这种关系对集合进行分类,凡是互相对等的集合就划入同一类这样,每一个集合都被划入了某一类任意一个集合A所属的类就称为集合A的基数,记作A或cardA这样,当A 与B同属一个类时,A与B 就有相同的基数,即A=B而当 A与B不同属一个类时,它们的基数也不同例如;古典文献学中总集别集丛书类书是常见的几种文献形式,它们各有特点,互相区别总集是集合多个作者的作品,如文选全唐诗而别集则专门收录单一作者的作品,例如庾子山集元稹集类书的概念在文献学中十分常见,它通过搜集群书的字词句子篇章,按照类别进行编辑,旨在方便;相同点通过索引访问集合中的元素,添加删除元素方法相同 4泛型集合DictionaryltK,V 它具有泛型的全部特性,编译时检查类型约束,获取元素时无需类型转换,并且它存储数据的方式和HashTable类似也是通过KeyValue对元素保存的定义语法为DictionaryltK,V对象名 = new DictionaryltK,V ltK,V中的K;集合是指具有某种特定性质的具体的或抽象的对象汇总而成的集体其中,构成集合的这些对象则称为该集合的元素数集指就是数的集合二者的区别1二者概念不同集合是指具有某种特定性质的具体的或抽象的对象汇总而成的集体数集指就是数的集合2二者从属关系不同集合的范围比数集的范围;第一个是空集,就是里边没有元素包括0也没有第二个是只有元素0的集合 第三个没见过,如果非得解释,那就是该集合是集合的集合有点绕,就是把空集作为元素,构成的集合。
Set 特点无元素插入顺序,不允许重复元素,元素位置由其HashCode决定 适用场景 需要避免重复元素且无需关注元素插入顺序的场景 需要频繁修改元素集合,如快速去重构建无序唯一元素集合等 插入和删除操作效率高,不会引起其常见的集合及其区别他元素变动的场景Map 特点用于存储键值对,提供高效的键;在集合论中,集合与集合之间的关系是数学研究的重要内容一个常见的表示方法是使用符号,例如“#8834”来表示一个集合是另一个集合的真子集假设有两个集合A和B,如果集合A中的所有元素都属于集合B,但集合B中至少有一个元素不属于集合A,则称集合A是集合B的真子集,写作A#8834B另一种。
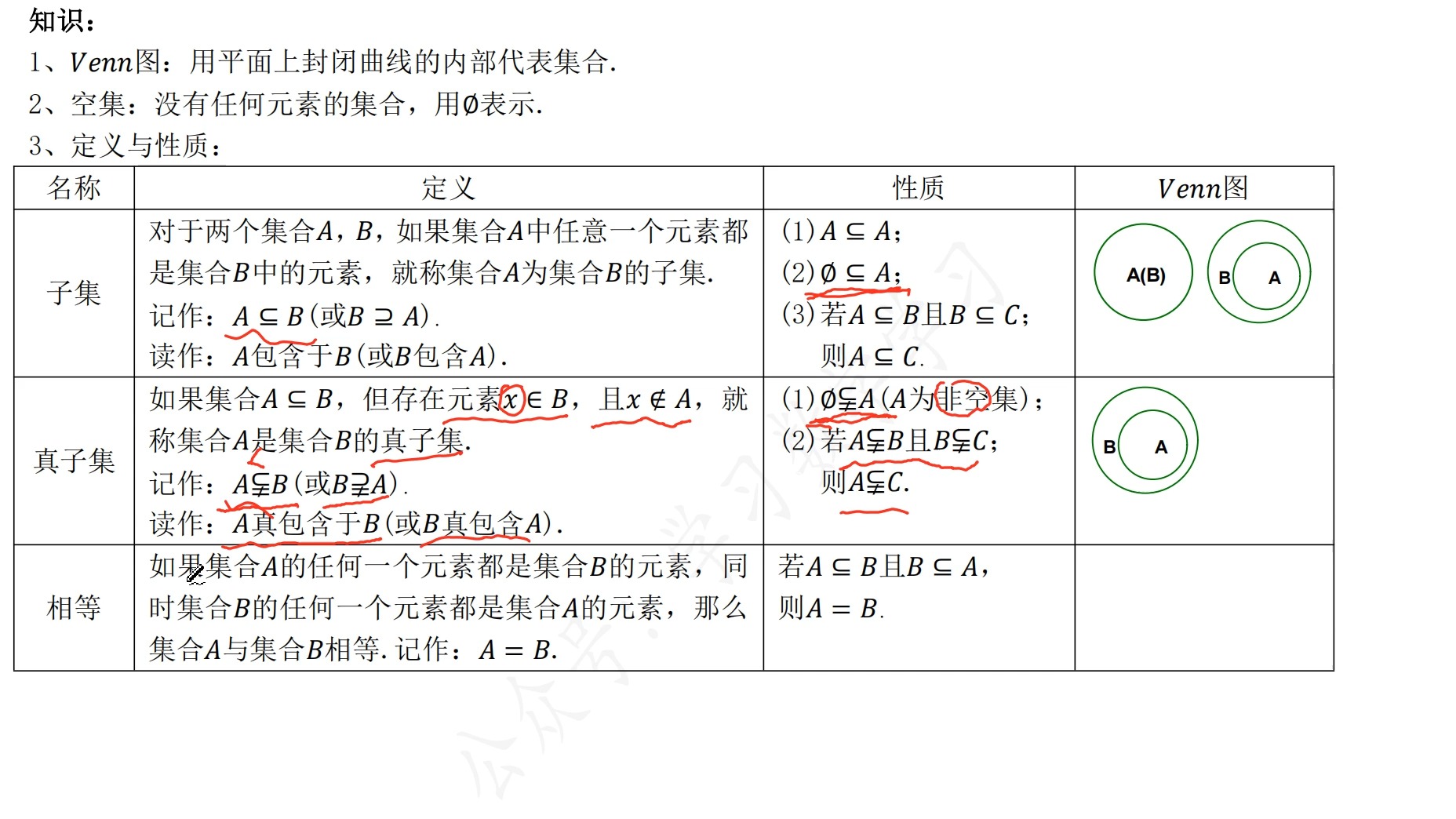
区别一集合的元素不同A真包含于B,A不可以等于BA包含于B,A可以等于B二概念不同如果集合A的元素是集合B的子集,并且B中至少有一个元素不属于A,那么集合A叫做集合B的真子集,记作A真包含于B或B真包含A如果集合A的任意一个元素都是集合B的元素,那么集合A叫做集合B的子集,记;1研究对象不同在集合论和有关的数学分支中,给定集合S的子集的搜集F叫做S的子集族或S上的集合族集合,简称集,是数学中一个基本概念,也是集合论的主要研究对象集合是指具有某种特定性质的具体的或抽象的对象汇总而成的集体其中,构成集合的这些对象则称为该集合的元素2性质不同集合。
